1. 개요(출처 : 위키백과)
로지스틱 회귀(영어: logistic regression)는 영국의 통계학자인 D. R. Cox가 1958년[1]에 제안한 확률 모델로서 독립 변수의 선형 결합을 이용하여 사건의 발생 가능성을 예측하는데 사용되는 통계 기법이다.
로지스틱 회귀의 목적은 일반적인 회귀 분석의 목표와 동일하게 종속 변수와 독립 변수간의 관계를 구체적인 함수로 나타내어 향후 예측 모델에 사용하는 것이다. 이는 독립 변수의 선형 결합으로 종속 변수를 설명한다는 관점에서는 선형 회귀 분석과 유사하다. 하지만 로지스틱 회귀는 선형 회귀 분석과는 다르게 종속 변수가 범주형 데이터를 대상으로 하며 입력 데이터가 주어졌을 때 해당 데이터의 결과가 특정 분류로 나뉘기 때문에 일종의 분류 (classification) 기법으로도 볼 수 있다.
흔히 로지스틱 회귀는 종속변수가 이항형 문제(즉, 유효한 범주의 개수가 두개인 경우)를 지칭할 때 사용된다. 이외에, 두 개 이상의 범주를 가지는 문제가 대상인 경우엔 다항 로지스틱 회귀 (multinomial logistic regression) 또는 분화 로지스틱 회귀 (polytomous logistic regression)라고 하고 복수의 범주이면서 순서가 존재하면 서수 로지스틱 회귀 (ordinal logistic regression) 라고 한다.[2] 로지스틱 회귀 분석은 의료, 통신, 데이터마이닝과 같은 다양한 분야에서 분류 및 예측을 위한 모델로서 폭넓게 사용되고 있다.
식[편집]
- 오즈 (odds) & 로짓 변환성공 확률이 실패 확률에 비해 몇 배 더 높은가를 나타내며 그 식은 아래와 같다.{\displaystyle {\text{odds}}={\frac {p(y=1|x)}{1-p(y=1|x)}}}
- 로짓 변환오즈에 로그를 취한 함수로서 입력 값의 범위가 [0,1] 일때 출력 값의 범위를 {\displaystyle (-\infty ,+\infty )}로 조정한다.{\displaystyle \operatorname {logit} (p)=\log {\frac {p}{1-p}}}
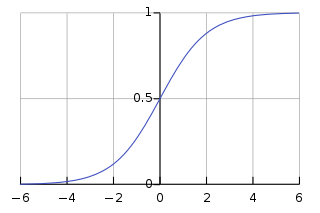
- 로지스틱 함수 (logistic function):로지스틱 함수의 그래프는 Figure 1과 같고 이는 독립 변수 x가 주어졌을 때 종속 변수가 1의 범주에 속할 확률을 의미한다. 즉, {\displaystyle {p(y=1|x)}}를 의미한다.로지스틱 함수는 로짓 변환을 통해 만들어지고, 그 형태는 다음과 같다.{\displaystyle {\text{logistic function}}={\frac {e^{\beta \centerdot X_{i}}}{1+e^{\beta \centerdot X_{i}}}}}
2. 내용
3. 기출문제
4. 기타(외우는 방법)
'교육 > 빅데이터분석자격증교육' 카테고리의 다른 글
| 데이터란? (0) | 2022.05.16 |
|---|---|
| 데이터베이터란? (0) | 2022.05.16 |
| 2장 데이터분석기획 설명자료 (0) | 2022.05.13 |
| 회귀분석이란(주식과 환율 상관관계 Python 코드포함)? (0) | 2022.05.13 |
| 의사결정나무(Decision Tree) (0) | 2022.04.26 |
